CSS/Funktionen/matrix()
Die CSS-Funktion matrix() definiert eine homogene 2D-Transformationsmatrix. Ihr Ergebnis ist ein Datentyp <Transformationsfunktion>
- anwendbar auf
- Parameter
- *
a b c dZahlenwerte, die die lineare Transformation beschreiben-
tx tyVerschiebung
-
matrix(a, b, c, d, tx, ty)
matrix(a, b, c, d, tx, ty) ist eine Zusammenfassung von matrix3d(a, b, 0, 0, c, d, 0, 0, 0, 0, 1, 0, tx, ty, 0, 1).Inhaltsverzeichnis
Siehe auch
Weblinks
- csswg: 13. Interpolation of Matrices CSS Transforms Module Level 2
- MDN: matrix()
- Browser-Support: caniuse.com
matrix()
Die Angabe transform="matrix(a,b,c,d,e,f)" transformiert ein Objekt mit Hilfe einer affinen Abbildung durch Angabe einer 3×3-Abbildungsmatrix  mit den sechs variablen Werten a, b, c, d, e und f.
mit den sechs variablen Werten a, b, c, d, e und f.
Dies entspricht der folgenden affinen Abbildung g, die den ursprünglichen Punkt mit den Koordinaten x und y wie folgt abbildet:
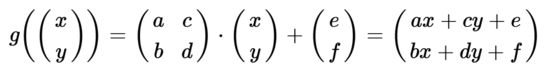
Man beachte die ungewöhnliche Position von b und c in der Abbildungsmatrix.
Die o. g. Standardtransformationen entsprechen dabei folgenden Matrizen:
| Änderung | Matrix |
|---|---|
| "nichts" (Identität) | matrix(1,0,0,1,0,0). Diese Angabe hat keinen Effekt.
|
translate(tx,ty)
|
matrix(1,0,0,1,tx,ty)
|
scale(sx,sy)
|
matrix(sx,0,0,sy,0,0)
|
rotate(α)
|
matrix(cos(α),sin(α),-sin(α),cos(α),0,0)1)
|
rotate(α,cx,cy)
|
matrix(cos(α),sin(α),-sin(α),cos(α),cx,cy) matrix(1,0,0,1,-cx,-cy), ausmultipliziertmatrix(cos(α), sin(α), -sin(α), +cos(α), (1-cos(α))*cx + sin(α)*cy, (1-cos(α))*cy - sin(α)*cx)
|
skewX(α)
|
matrix(1,0,tan(α),1,0,0)
|
skewY(α)
|
matrix(1,tan(α),0,1,0,0)
|
- 1) Eigentlich entspricht diese Drehmatrix der Drehung gegen den Uhrzeigersinn während
rotateim Uhrzeigersinn dreht, sodass der Parameter der trigonometrischen Funktionen -α statt α sein müsste. Jedoch ist in SVG die y-Achse falschherum, wodurch sich dies gegenseitig aufhebt.
Verkettung berechnen
Die Verkettung von zwei matrix()-Funktionen – auch hier gilt, dass die Transformationen von rechts nach links durchgeführt werden – kann durch die Multiplikation der beiden Matrizen, diesmal von links nach rechts, erfolgen. Für zwei Transformationen mit "matrix" gilt:
transform="matrix(a2 b2 c2 d2 e2 f2) matrix(a1 b1 c1 d1 e1 f1)"
entspricht
Mges = M2 * M1
und damit der Gesamtmatrix
transform="a1*a2+c1*b2, b1*a2+d1*b2, a1*c2+c1*d2, b1*c2+d1*d2, a1*e2+c1*f2+e1, b1*e2+d1*f2+f1"
Bei mehr als zwei Transformationen
transform="matrix(an bn cn dn en fn) ... matrix(a2 b2 c2 d2 e2 f2) matrix(a1 b1 c1 d1 e1 f1)"
gilt
Mges = Mn * ... * M2 * M1
(von links nach rechts).
Eine derartige Verkettung kann auch durch Gruppierung entstehen:
<g transform="matrix(a2 b2 c2 d2 e2 f2)">...<path transform="matrix(a1 b1 c1 d1 e1 f1)" ... />...
</g>
matrix() und matrix3D()
Bei den CSS Transform-Funktionen handelt es sich, mathematisch gesagt, um lineare Abbildungen. In der mathematischen Disziplin der Linearen Algebra werden solche Abbildungen durch Zahlentabellen dargestellt, die angeben, wie die Koordinaten eines Punktes miteinander zu verrechnen sind, um die Koordinaten des gewünschten Zielpunktes zu erhalten. Eine solche Tabelle nennt man eine Matrix. Sie hat genauso viele Zeilen wie Spalten (sie ist quadratisch) und für eine Operation in n Dimensionen braucht eine Matrix ebenso viele Zeilen und Spalten.
Überraschenderweise ist eine zweidimensionale Verschiebung (translate) aber nicht als zweidimensionale lineare Abbildung darstellbar. Mit dem Trick, einem zweidimensionalen Koordinatenpunkt eine Z-Koordinate mit dem Wert 1 anzuhängen und eine dreidimensionale Matrix zu verwenden, lässt sich das Problem lösen. Solange der zu transformierende Punkt dabei in der Z=1 Ebene bleiben soll, sind von den 9 Werten dieser dreidimensionalen Matrix drei immer gleich. Sie sieht so aus:
scaleX skewY transX
skewX scaleY transY
0 0 1
Die Werte in der Matrix tun genau das, was ihr Name besagt. scaleX/scaleY sind die Skalierungsfaktoren in X und Y-Richtung, transX/transY ist die Verschiebung in X und Y Richtung und skewX/skewY die Abschrägung, allerdings nicht in Grad, sondern in Prozent. Ein skewX-Wert von 1 (100%) schrägt eine Figur entlang einer 45° Geraden ab. Die dritte Zeile der Matrix ist immer 0 0 1.
Eine solche Matrix entspricht der folgenden Umrechnung des Punktes (x, y, 1) auf (x', y', 1):
x' = scaleX·x + skewY·y + transX
y' = skewX·x + scaleY·y + transY
Interessanterweise lässt sich durch eine geschickte Kombination von scaleX/scaleY und skewX/skewY auch eine Rotation darstellen. Mit scaleX=scaleY=cos(α), skewY=-sin(α) und skewX=sin(α) entsteht eine Drehung um den Winkel α.
Die CSS Funktion matrix() tut nun nichts weiter, als die Werte ersten beiden Zeilen der Transformationsmatrix aufzunehmen, und zwar spaltenweise. Die folgende Matrix spiegelt das Element, auf das sie angewendet wird, horizontal (scaleX=-1), schrägt es um 50% nach rechts ab (skewX=-0.5) und verschiebt es um 100 Pixel nach rechts (transX=100):
-1 0 100
-0.5 1 0
0 0 1
Als CSS Transform würden Sie das als transform: matrix(-1, -0.5, 0, 1, 100, 0); notieren. Da die letzte Zeile immer 0 0 1 ist, wird sie bei der Übergabe an matrix() weggelassen.
Komplexere Transformationen lassen sich mit Hilfe einer Matrizenmultiplikation aus ihren einzelnen Schritten zusammensetzen. Beispielsweise können Sie eine Drehung um 20 Grad um den Punkt (50,100) so realisieren, dass Sie das Objekt zuerst so schieben, dass der Drehpunkt in (0,0) liegt (translate(-50,-100)), dann drehen (rotate(20deg)) und wieder zurückschieben (translate(50,100)). Das sind drei Transformationsmatrizen:
M3 M2 M1
translate(50,100) rotate(20deg) translate(-50,-100) Produkt
1 0 50 0.940 -0.342 0 1 0 -50 0.940 -0.342 37.22
0 1 100 0.342 0.940 0 0 1 -100 0.342 0.940 -11.07
0 0 1 0 0 1 0 0 1 0 0 1
Die Matrizen sind „falsch herum“ aufgeschrieben. Das liegt daran, dass in einer Matrizenmultiplikation die Matrix, die am weitesten rechts steht, der zuerst angewendeten Transformation entspricht. Aus dem gleichen Grund werden auch die Transform-Funktionen, die Sie in einer transform-Eigenschaft verketten, von rechts nach links ausgeführt. Die Matrizenmultiplikation ist assoziativ, aber nicht kommutativ; wenn Sie das Matrixprodukt nachrechnen wollen, können Sie also nach Belieben (M3·M2)·M1 oder M3·(M2)·M1) rechnen, aber keinesfalls die Reihenfolge der Matrizen verändern.
Die beiden folgenden CSS Angaben sind demnach gleichwertig (unter der Voraussetzung, dass transform-origin auf 0 0 bzw. top left gesetzt ist):
transform: translate(-50px, -100px) rotate(20deg) translate(50px, 100px); transform: matrix(0.940, 0.342, -0.342, 0.940, 20.116, -14.086);
Die matrix3d() Funktion tut vergleichbares. Für Transformationen im dreidimensionalen Raum benötigt man allerdings eine vierdimensionale Matrix, und die Koeffizienten sind auch nicht mehr so einfach ableitbar. Deswegen hat matrix3d() 16 Parameter, für jede Zahl der Matrix einen. Auch hier wird die Matrix spaltenweise in Argumente für die CSS-Funktion übertragen. Für eine Diskussion der Matrizen, die Sie als Bausteine für 3D-Transformationen verwenden können, lesen Sie bitte in den angegebenen Quellen nach.
Solange Sie Ihre Transformation mit einer Verkettung von CSS Transformationsfunktionen zusammensetzen können, gibt es keinen Grund, die matrix- oder matrix3d-Funktion zu nutzen. Letztlich erzeugt browserintern jede Transformationsfunktion die entsprechende Matrix, und die Verkettung der Funktionen erzeugt das Matrixprodukt. Der Browser kann das aber viel schneller berechnen, als Sie das mit JavaScript tun könnten.
Erst dann, wenn Sie sich eine lineare Transformation ausdenken, die sich mit den verfügbaren Basisfunktionen nicht mehr erzeugen lässt, benötigen Sie die matrix() bzw. matrix3d(). Nichtlineare Transformationen (d.h. worin Koordinatenwerte mit einem Exponenten eingehen) sind mit CSS nicht machbar.
Es gibt einen Umrechner, obwohl solch ein Feintuning bezüglich der Stylesheet-Größe wohl nicht den Aufwand lohnt:
- meyerweb.com: The Matrix Resolutions (Umrechner von „normalen“ Transformationen in eine Matrix.
Siehe auch:

