JavaScript/Objekte/Math/atan2
Die Methode Math.atan2(y,x) erwartet als Parameter zwei Zahlen. Diese beschreiben die x- und y-Koordinaten eines Punktes P in der Zahlenebene, und atan2 berechnet den Winkel zwischen der Verbindungsgerade durch (0,0) und P und der positiven X-Achse als Wert im Bogenmaß im Bereich -π bis π (Vollkreis).
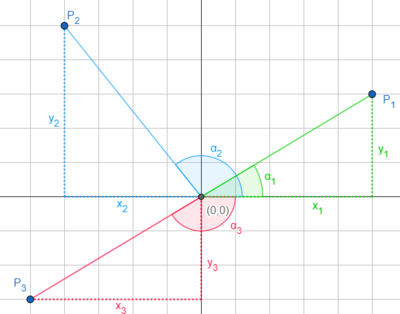
Ein Anwendungsfall von Math.atan2() ist die Umrechnung von kartesischen (rechtwinkligen) Koordinaten in Polarkoordinaten (Angabe von Winkel zu einer Bezugslinie und Abstand zum Mittelpunkt). Beispielsweise hat der Punkt P1 im nebenstehenden Bild die Koordinaten (5|3). Der Winkel α1 beträgt etwa 31°. Rufen Sie Math.atan2(3, 5) auf, erhalten Sie 0.5404, was 31° im Bogenmaß entspricht.
document.addEventListener("click", function(mouseEvent) {
// Mausposition relativ zum Mittelpunkt des Body bestimmen
let dy = mouseEvent.clientY - document.body.clientHeight/2,
dx = mouseEvent.clientX - document.body.clientWidth/2;
// Winkel und Abstand zum Mittelpunkt bestimmen (Polarkoordinaten)
let winkel = Math.atan2(dy, dx) / Math.PI * 180;
let abstand = Math.hypot(dy, dx);
console.log(`Ihr Klick befindet sich bei ${winkel} Grad und ist ${abstand}px vom Mittelpunkt entfernt.`);
}
Motivation für die Existenz von atan2
Für den Fall, dass x ≧ 0 ist, lässt sich dieser Winkel auch mit Math.atan(y/x) berechnen. Dies funktioniert sogar noch für x = 0, weil JavaScript bei einer Division durch 0 nicht abbricht, sondern die speziellen Werte +Infinity und -Infinity liefert, die Math.atan korrekt mit 𝜋/2 bzw. -𝜋/2 beantwortet.
Da aber die tan-Funktion für die Winkel von 180° bis 360° (bzw. von -180° bis 0°) die gleichen Werte liefert wie für 0° bis 180°, lässt sich mit atan(y/x) nicht auf alle vier Quadranten der Zahlenebene zurückschließen. Der Punkt P1 im obigen Bild hat zum Beispiel die Koordinaten (5,3), der Winkel α1 könnte also mit Math.atan(3/5) berechnet werden (es sind 0,5404rad, ungefähr 31°). Allerdings hat der diagonal gegenüberliegende Punkt P3 (-5, -3) ebenfalls 0,6 als Verhältnis y/x, die atan-Funktion würde hier ebenfalls 0,5404rad zurückliefern.
Die Math.atan2 Funktion schafft Abhilfe, indem sie nicht das Verhältnis y/x als Argument erwartet, sondern y und x selbst, wodurch die Vorzeichen von y und x erhalten bleiben und der vollständige 360° Kreis erfasst werden kann. Math.atan2(-3,-5) gibt -2,6012 zurück, was -149° entspricht.
Verfügbarkeit
Die Methode Math.atan2 ist seit 1999 Teil des JavaScript Standards und ist überall verfügbar, wo auch Math.atan verfügbar ist. Einige alte Android-Browser (vor Version 4.4) kennen atan2 nicht, dort fehlt aber das komplette Trigonometriepaket, so dass Sie sich dort mit einem Nachprogrammieren des entsprechenden Taylorreihen behelfen müssten.
