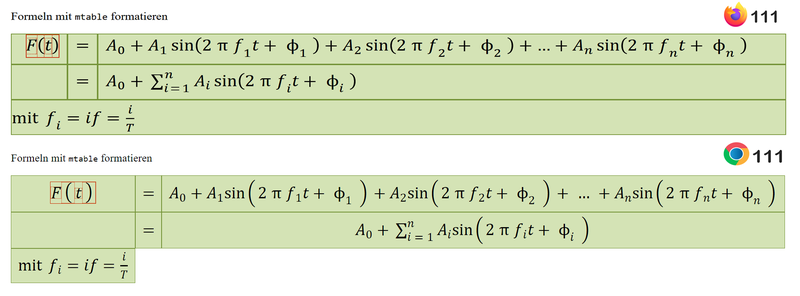MathML/Einsteiger-Tutorial
Mit MathML können Sie mathematische Zeichen, Ausdrücke und Formeln im Web darstellen. Diese sind frei skalierbar und immer gestochen scharf, sowie auch für Screenreader (vor)-lesbar.
Mittlerweile (Stand März 2023) unterstützen alle großen Browser MathML.
Dieses Tutorial zeigt die wichtigsten Elemente in MathML und wie sie in Webseiten eingebunden werden. Dabei verwendet SELFHTML MathML Core, das die beste Integration in HTML und CSS bietet. [1][2]
Inhaltsverzeichnis
math - Das Top-Level-Element
Ein mathematischer Ausdruck muss in das math-Element innerhalb des body eingefügt werden.
<math xmlns="http://www.w3.org/1998/Math/MathML"> … </math> kann in HTML5 weggelassen werden.Abgesetzte Formeln
Ein mathematischer Ausdruck kann im Fließtext erscheinen („inline“) oder vom Fließtext abgesetzt werden.
In MathML ist für diese Darstellungsmodi das display-Attribut des <math>-Elements zuständig. Es entspricht weitgehend der display-Eigenschaft in CSS.
-
inline: Formeln werden innerhalb des Fließtexts gerendert (Defaultwert) -
block: Formeln werden zentriert als eigenes Block-Element gerendert.
<math display="inline"> ... </math>
<math display="block"> ... </math>
Sie können display entweder als HTML-Attribut oder über CSS festlegen. Über CSS wird es allerdings ohne weitere Festlegung nicht zentriert.
MathML
Basis-Elemente
Die darzustellenden Zeichen sind als Text in eines der folgenden Basis-Elemente (engl. token elements) einzufügen:
- <mi> für Bezeichner wie Variablen und Konstanten, z.B.
<mi>x</mi>für „x“;
Sie werden defaultmäßig kursiv dargestellt,
Funktionsbezeichner wie sin, cos mit mehreren Glyphen jedoch normal. - <mn> für Zahlwerte, also z.B.
<mn>2</mn>für „2“; - <mo> für mathematische Operatoren und Rechenzeichen, also z.B.
-
<mo>+</mo>für „+“, <mo>-</mo>für „-“ oder<mo>=</mo>für „=“.
-
Diese Basiselemente sind für jeden Ausdruck in MathML notwendig und bestimmen die Schriftsetzung der beinhalteten Zeichen. Die Elemente <mn> und <mo> können mehrere Zeichen beinhalten, <mi> dagegen nur einbuchstabige Variablen.
<mi>-Element eine Variable mit nur einer Glyphe mit Leerzeichen umschließen, sollte der Browser dies als eine Glyphe erkennen und kursiv darstellen.Chrome, Edge und Opera zählen den Whitespace jedoch mit und geben die Variable normal aus!
Als erstes „Hallo-Welt-Beipiel“ in MathML betrachten wir den länglichen, aber strukturell einfachen Ausdruck:
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mn>4</mn>
<mi>x</mi>
<mo>+</mo>
<mn>4</mn>
<mo>=</mo>
<mo>(</mo>
<mn>2</mn>
<mo>+</mo>
<mn>2</mn>
<mo>)</mo>
<mi>x</mi>
<mo>+</mo>
<mn>2</mn>
<mo>·</mo>
<mn>2</mn>
</math>
Diese Gleichung 4x + 4 = (2 + 2)x + 2 · 2 könnte auch (noch) mit „normalem“ Text notiert werden - komplexere Ausdrücke jedoch nicht mehr.
In der vorletzten Zeile wird als Malzeichen ein Punkt verwendet, der als Zeichen-Entität-Referenz · notiert wird. Einfacher wäre dieses Zeichen: ·
Information: Exkurs: unsichtbare Multiplikationszeichen
In der Mathematik gibt es die Konvention, dass bei der Multiplikation einer Zahl mit einer Variable wie z. B.4x die Multiplikationszeichen weggelassen werden können. In MathML können Sie sie aber auch (unsichtbar) notieren, ein Screenreader liest sie dann vor:
<mn>4</mn>
<mo>⁢</mo>
<mi>x</mi>
Brüche
Mathematische Formeln unterscheiden sich von normalem Fließtext dadurch, dass sie durchaus mehrzeilig sein können, um die Übersicht zu erhöhen. Bestes Beispiel sind Brüche in der „Zähler-Bruchstrich-Nenner-Schreibweise“:
Ein Bruch wird mit dem <mfrac>-Element erzeugt. Dieses erwartet zwei Parameter:
<mfrac> Zähler Nenner </mfrac>
<mfrac>
<mi>Z</mi>
<mi>N</mi>
</mfrac>
<mtext> z. B. </mtext>
<mfrac>
<mn>1</mn>
<mi>x</mi>
</mfrac>
Im Beispiel gibt es zwei Brüche, die jeweils mit dem mfrac-Element ausgezeichnet worden sind. Während der erste Bruch nur aus zwei Variablen innerhalb eines mi-Elements besteht, besteht der Zähler des zweiten Beispiels aus einer mit mn ausgezeichneten Zahl.
Die beiden Brüchen werden durch einen kurzen Zusatztext ergänzt, der in einem <mtext>-Element steht.
Bestehen Zähler oder Nenner nicht nur aus einer Zahl, sondern aus einem komplexeren Rechenausdruck, so sind sie mit <mrow> zu Einheiten zu gruppieren. mrow entspricht dabei einem inhaltsleeren div oder g-Element (in SVG), um mehrere Basis-Elemente oder auch ganze Terme zusammenzufassen, bzw. in eine Reihe zu „zwingen.“
<mi>f</mi>
<mi>x</mi>
<mi>y</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mn>13</mn>
<mi>x</mi>
<mo>-</mo>
<mn>37</mn>
</mrow>
<mrow>
<mn>2</mn>
<mi>y</mi>
<mo>+</mo>
<mn>1</mn>
</mrow>
</mfrac>
Das Beispiel besteht aus einem Bruch. Die beiden Kindelemente sind mrow-Elemente, die jeweils einen Term enthalten.
<math>
<mrow>
<mi>Φ</mi>
<mo>=</mo>
<mfrac>
<mi>a</mi>
<mi>b</mi>
</mfrac>
<mo>=</mo>
<mfrac>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
<mi>a</mi>
</mfrac>
<mo>=</mo>
<mfrac>
<mrow>
<mi>1</mi>
<mo>+</mo>
<msqrt>
<mi>5</mi>
</msqrt>
</mrow>
<mi>2</mi>
</mfrac>
<mo>≈</mo>
<mi>1,618…</mi>
</mrow>
</math>
Exponenten und Indizes
Ausdrücke werden hoch- oder tiefgestellt durch das Element <msup> für Exponenten und <msub> für Indizes.
<msub>
<mi>y</mi>
<mn>0</mn>
</msub>
<mo>=</mo>
<msup>
<mi>x</mi>
<mn>2</mn>
</msup>
<msup> base superscript </msup>Auch komplexere Terme können im Exponenten dargestellt werden, sie müssen allerdings mit <mrow> gruppiert werden:
<mi>y</mi>
<mo>=</mo>
<msup>
<mi>x</mi>
<mrow>
<mn>2</mn>
<mi>k</mi>
<mo>+</mo>
<mn>1</mn>
</mrow>
</msup>
<h1>Der Satz des Pythagoras</h1>
<math>
<mrow>
<msup><mi>a</mi><mn>2</mn></msup>
<mo>+</mo>
<msup><mi>b</mi><mn>2</mn></msup>
<mo>=</mo>
<msup><mi>c</mi><mn>2</mn></msup>
</mrow>
</math>
Wurzelausdrücke
Wurzelziehen oder Radizieren (von lat. radix „Wurzel“; vgl. Radieschen und Rettich) ist eine Umkehrung des Potenzierens.
Für Quadratwurzeln wird das <msqrt>-Element verwendet:
<msqrt>
<mn>1</mn>
<mo>-</mo>
<mfrac>
<mi>x</mi>
<mn>2</mn>
</mfrac>
</msqrt>
Innerhalb der Quadratwurzel befinden sich mehrere Basis-Elemente und ein Bruch. Diese werden nacheinander dargestellt.
Um andere Wurzelexponenten als 2 verwenden, also eine Kubikwurzel oder den Wurzelexponent durch eine Variable darzustellen, gibt es in MathML das <mroot>-Element, das zwei Unterelemente erwartet, zunächst den Term, aus dem die Wurzel zu ziehen ist, und dann den Wurzelexponent:
<mroot>
<mrow>
<mn>1</mn>
<mo>-</mo>
<mfrac>
<mi>x</mi>
<mn>2</mn>
</mfrac>
</mrow>
<mn>3</mn>
</mroot>
Da das mroot-Element nur zwei Parameter erwartet, wird der Radikand wieder in ein mrow-Element geschachtelt. Anschließend folgt im letzten Kindelement der Wurzelexponent, hier 3.
<math display="block">
<mrow>
<mi>x</mi>
<mo>=</mo>
<mo>-</mo>
<mfrac>
<mi>p</mi>
<mn>2</mn>
</mfrac>
<mo>±</mo>
<mfrac>
<mn>1</mn>
<mn>2</mn>
</mfrac>
<msqrt>
<mrow>
<msup>
<mi>p</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mi>q</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
</math>
Summen und Integrale
Die Grenzen von Summen und Integralen werden in MathML durch das <munderover>-Element ermöglicht. Es erwartet drei Elemente in der Reihenfolge Symbol (Summe ∑ oder Integral ∫, ...), die untere Grenze und die obere Grenze.
<munderover>
<mo>∫</mo>
<mn>1</mn>
<mn>e</mn>
</munderover>
<mfrac><mrow><mo>d</mo><mi>x</mi></mrow><mi>x</mi></mfrac>
<mo>=</mo>
<mn>1</mn>
Will man eine der Grenzen nicht angeben, so muss an die Stelle ein leeres Element <mn></mn> gesetzt werden. Bei den Grenzen für Summen gibt es eine Besonderheit, hier wird zwischen den Darstellungsmodi inline und display unterschieden.
<mrow displaystyle="true">
<munderover>
<mo>∑</mo>
<mn>1</mn>
<mn>2</mn>
</munderover>
<mfrac><mn>1</mn><mi>k</mi></mfrac>
<mo>=</mo>
<mn>1,5</mn>
</mrow>
Der Quelltext ergibt im Fließtext ∑ 1 2 1k = 1,5 , d.h. die Grenzen sind neben dem Summenzeichen angeordnet. Möchte man die Grenzen oberhalb und unterhalb von ihm haben, also ∑ 1 2 1k = 1,5 , so kann man das durch Einfügen des Terms in das Element <mrow displaystyle="true"> erreichen:
<mstyle displaystyle="true">
<munderover>
<mo>∑</mo>
<mn>1</mn>
<mn>2</mn>
</munderover>
<mfrac><mn>1</mn><mi>k</mi></mfrac>
<mo>=</mo>
<mn>1,5</mn>
</mstyle>.
Im Gegensatz dazu werden für Formeln im abgesetzten Modus die Grenzen standardmäßig immer ober- und unterhalb angeordnet, wie wir anhand der Gleichungen von Euler und Riemann ersehen:
<math mode="display">
<mi>ζ</mi> <mo>(</mo><mi>s</mi><mo>)</mo>
<mo>=</mo>
<munderover>
<mo>∑</mo>
<mrow><mi>n</mi><mo>=</mo><mn>1</mn></mrow>
<mi>∞</mi>
</munderover>
<mfrac>
<mn>1</mn>
<msup><mi>n</mi><mi>s</mi></msup>
</mfrac>
<mo>=</mo>
<munderover>
<mo>∏</mo>
<mrow><mi>p</mi><mo>∈</mo><mn>ℙ</mn></mrow>
<mn></mn>
</munderover>
<mfrac>
<mn>1</mn>
<mrow><mn>1</mn><mo>-</mo><msup><mi>p</mi><mrow><mo>-</mo><mi>s</mi></mrow></msup></mrow>
</mfrac>
<mo>=</mo>
<mfrac>
<mrow>
<msup><mn>e</mn><mrow><mo>-</mo><mn>i</mn><mn>π</mn><mi>s</mi></mrow></msup>
<mn> </mn>
<mn>Γ</mn><mo>(</mo><mn>1</mn><mo>-</mo><mi>s</mi><mo>)</mo>
</mrow>
<mrow>
<mn>2</mn><mn>π</mn><mn>i</mn>
</mrow>
</mfrac>
<munderover>
<mo>∫</mo>
<mi>C</mi>
<mn></mn>
</munderover>
<mfrac>
<mrow><msup><mi>z</mi><mrow><mi>s</mi><mo>-</mo><mn>1</mn></mrow></msup><mo>d</mo><mi>z</mi></mrow>
<mrow><msup><mn>e</mn><mi>z</mi></msup><mo>-</mo><mn>1</mn></mrow>
</mfrac>
<mn> </mn><mn> </mn>
<mo>(</mo><mi>s</mi><mo>∈</mo><mn>ℂ</mn>
<mo>,</mo><mn> </mn>
<mo>Re</mo><mi>s</mi><mo>></mo><mn>1</mn>
<mo>)</mo>
</math>
Hierbei ist ζ die Zeta-Funktion, ℙ die Menge der Primzahlen, Γ die Gammafunktion Γ(s) = ∫0∞ ts-1 e-t dt und C ein Weg in der komplexen Ebene, der bei +∞ beginnt, den Ursprung im positiven Sinn einmal umkreist, ohne die Punkte ±2πi, ±4πi, ..., zu durchlaufen, und schließlich nach +∞ zurückkehrt.[3]
Matrizen und Tabellen
Eine Matrix (Plural Matrizen) eine rechteckige Anordnung (Tabelle) von Elementen (meist mathematischer Objekte, etwa Zahlen). Rechteckig bedeutet, dass die Anordnung der Elemente stattfindet in Zeilen und Spalten. Um Matrizen zu schreiben, benötigen wir das Tabellenelement <mtable>
<mtable>
<mtr>
<mtd><mn>0</mn></mtd>
<mtd><mo>-</mo><mn>i</mn></mtd>
</mtr>
<mtr>
<mtd><mn>i</mn></mtd>
<mtd><mn>0</mn></mtd>
</mtr>
</mtable>
Wie man sieht, ist <mtable> genauso strukturiert wie eine HTML-<table>, nur eben jeweils mit dem obligatorischen m als Präfix der Elementnamen.
Statt der runden Klammern kann man auch beliebige andere Klammern verwenden, z.B. eckige oder geschweifte Klammern:
<mrow>
<mo>[</mo>
<mtable>
<mtr>
<mtd><mi>cos</mi> <mi>x</mi></mtd>
<mtd><mo>-</mo><mi>sin</mi> <mi>x</mi></mtd>
</mtr>
<mtr>
<mtd><mi>sin</mi> <mi>x</mi></mtd>
<mtd><mi>cos</mi> <mi>x</mi></mtd>
</mtr>
</mtable>
<mo>]</mo>
</mrow>
Tabellenlayout
In der Frühzeit des Webdesigns in den 90ern - als größere Monitore mit höheren Auflösungen auf den Markt kamen, wurden HTML-Tabellen dazu zweckentfremdet, Inhalte nebeneinander darzustellen.
Auch wenn MathML heute mit CSS formatiert werden kann, sind Positionierungen mit CSS nur schwierig bis gar nicht möglich, sodass zumindest derzeit wieder auf Tabellen zur Layout-Gestaltung zurückgegriffen werden muss:
<mtable columnalign="left">
<mtr>
<mtd columnalign="right" class="term">
…
</mtd>
<mtd>
…
</mtd>
<mtd>
…
</mtd>
</mtr>
<mtr>
…
</mtr>
<mtr>
<mtd columnspan="3" colspan="3">
…
</mtd>
</mtr>
</mtable>
Im Beispiel finden sich zwei Formeln, wobei in der zweiten Zeile kein Term links des Gleichheitszeichens vorhanden ist.
Um die zweite Zeile einzurücken, wurde eine Tabelle erstellt, deren erstes Tabellenfeld in der zweiten Zeile leer bleibt.
Die dritte Zeile dient nur zur Ergänzung und ist keine Fortführung der Gleichung. Deshalb soll sie sich mit colspan="3" über drei Tabellenfelder erstrecken. (Die alte Schreibweise columnspan="3" funktioniert nur im Firefox, die neue in keinem Browser!)
Wie Sie sehen, werden die Attribute nur im Firefox beachtet, Chrome, Edge und Opera ignorieren sie (Stand: März 2023). Dadurch wächst die Breite der ersten Spalte auf die Breite des gesamten Terms - eine Lösung wäre es, in der dritten Zeile zwei leere mtd-Felder einzufügen und die Gleichung im dritten Tabellenfeld zu notieren.
Im Algebra-Tutorial findet sich ein weiterer Versuch:
Die Breitenangabe wird im Firefox 111 ignoriert; im Chrome funktioniert es, allerdings werden die Logarithmen nicht mehr inline dargestellt. Im Live-Beispiel wurden diese deshalb in einem weiteren mrow-Element geschachtelt.
Zeilenumbruch in MathML
MathML ist in Grenzen responsiv. Formeln, die das Ende des verfügbaren Platzes erreichen, brechen um und beginnen auf der nächsten Zeile.
Eine manuelle Steuerung durch den Webentwickler ist kaum möglich:
-
<mspace linebreak='newline' />ist in keinem Browser implementiert und aus MathML Core herausgefallen.[4]
Einrückung von Textzeilen
Hier gibt es einige Möglichkeiten, die aber alle ihre Nachteile haben oder in den Browsern nicht implementiert sind.
- mspace ermöglicht es einen Leerraum zu setzen. Allerdings müsste man die Werte als Magic Number ins Markup setzen.
- <mpadded> würde das Gleichheitszeichen umschließen, gehört aber zu den Legacy Compat(ibility)-Elementen, die aber sowieso nicht mehr verwendet werden sollten. Allerdings müsste man auch hier die Werte als Magic Number ins Markup setzen
- <mphantom> würde es ermöglichen, die obere Formel zu notieren, deren Platz auszufüllen, wobei die Formel aber unsichtbar bleibt. Dieses Element ist aber ebenfalls obsolet.
- in MathML 3.0 gab es einen Versuch[5], der aber nie implementiert wurde:
<math xmlns='http://www.w3.org/1998/Math/MathML'
maxwidth='200px' linebreakmultchar='×' linebreakstyle='before'
indentalign='id' indenttarget='firstOperator'>
<mrow>
<mrow>
<mo>(</mo>
<mrow>
<msup>
<mi>x</mi>
<mn>4</mn>
</msup>
<mo id='firstOperator'>-</mo>
…
</math>
Fazit
Formeln in MathML werden von allen Browsern optisch ansprechend gerendert. Hier kann man den Default-Stylesheets der Browser vertrauen.
Will man aber komplexere Formeln individuell gestalten, stößt man bald auf unüberwindliche Schwierigkeiten. Hier hilft es nur die Formeln auf einzelne math-Elemente aufzuteilen und sie als HTML-Elemente mit CSS wie gewünscht zu verschieben.
Siehe auch
Weblinks
- ↑ W3C: MathML Core
- ↑ Das vorliegende Tutorial ist eine Neubearbeitung des Kurztutorial MathML von Andreas de Vries aus dem Jahre 2012
- ↑ Vgl. E.C. Titchmarsh & D.R. Heath-Brown: The Theory of the Riemann Zeta-function. Clarendon Press, Oxford 1986, Eqn. (2.4.2), sowie J. Neukirch: Algebraic Number Theory. Springer-Verlag, Berlin Heidelberg 1999, §VII.1.
- ↑ bugzilla: [MathML3] Improve MathML linebreaking
- ↑ Controlling indentation (wiris.com)